監督和非監督式學習使用了所有的資料來學習進行預測,但是在強化學習中,並非所有資料從一開始就看得見,而是透過摸索的形式和環境互動取得經驗,從錯誤中學習找到一個長期的最佳行動,也就是做出決策。
強化學習是建立在馬爾可夫決策過程的架構之上,組成如下。
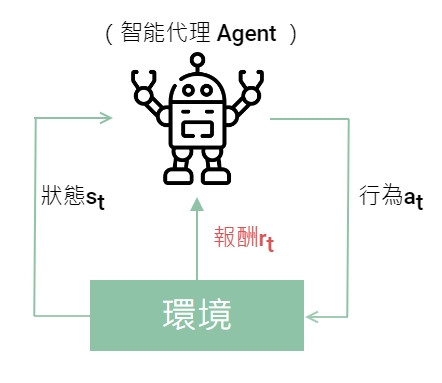
以自駕車(Agent)為例,先用影像辨識和感測器觀察周遭環境有哪些其他物體,自己在道路的什麼位置取得狀態
,以此為依據選擇了行為
用一個速率向前開,如果碰撞到物體就是得到負的報酬,沒有碰撞而且透過 GPS 計算更接近目的地就得到正的報酬
,透過報酬作行為的修正。此時來到新的時間
,重新觀察新的環境有沒有其他車子或行人在附近,重複循環。
這個架構在狀態變化時假定有馬爾可夫性質(Markov property),也就是未來的狀態僅依賴現在狀態,不考慮過去的狀態。 只依賴
,不考慮
,
造成的影響。
因為未來狀態如果不只考慮現在狀態,還要考慮前一個,前前一個狀態給予的影響會沒完沒了,太複雜了,但也不是說之前的就沒影響,畢竟現在的狀態也是過去狀態造成的。
最終把每次得到的報酬加總起來最大化就是學習的目標。也就是最大化累積報酬。
但由於有時間這個概念,每次的報酬在做加總時還會乘上當時的折舊率(discount rate)。畢竟未來的報酬太遙遠,現在的100元和未來的100元相比,一定是現在的100元比較有影響力。
...
選擇行動時,有複數選項要選哪個比較好呢?
我們希望累積報酬最大,所以每次選擇的行動(做出的決策)都有他的理由存在。
而吃角子老虎機就是一個如何在探索和利用間取得平衡的一種策略(Policy)
吃角子老虎機是一個拉一個搖桿出現相同圖案就中獎的賭博機,而很多台吃角子老虎機象徵同時有好幾個選擇。

—— 吃角子老虎機,圖片出處:多腕バンディット入門
具體有以下兩個方法
你有聽說過柏青哥有容易中獎和不容易中獎的機台嗎?吃角子老虎機也是一樣,如果你今天的錢可以投100次硬幣,我們用
(探索率)=10%,也就是前10次讓你去挑選一台老虎機去拉搖桿看看(探索),當你找到了其中最容易中獎的機台,那剩下90次就通通玩那個機台就好(利用),可以說是賭徒的智慧。
實際用程式跑看看,三台老虎機 A,B,C 隱藏的中獎期望值為 70%,50%,30%: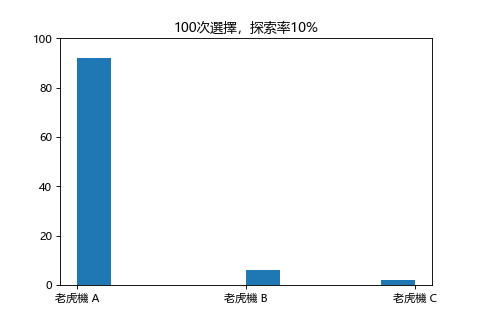
儘管玩家不知道隱藏的機率,但是透過這個策略,自然而然會把錢都用在老虎機 A。
以剛才的貪婪策略來說,探索(找易中獎機台)次數過多會使得利用次數過少,反之探索過少可能會漏掉超容易中獎的機台,所以好一點的方法是兼顧當前利益和探索次數的算法,也就是 UCB 策略。
簡單來說 分數 = 中獎率 + Bonus ,Bonus 是被選的次數越少數值越高,而中獎率高的老虎機如果一直被選擇,導致 Bonus 逐漸變低,直到分數低於其他台,就選擇其他分數高的老虎機。也就是雖然這台中獎率可能最高,偶爾也要給其他機台一點機會的概念。(除非這台中獎機率高到沒有 Bonus 也比其他台的分數高。)
Bonus 為什麼選越多次會越來越少,因為選越多次代表目前中獎概率越趨近這台實際的中獎概率,還記得硬幣拋了無數次正反面的出現機率會逼近理論值的一半一半嗎,因此這台選了那麼多次,大概的中獎分布已經看得出來,而其他台還沒選那麼多次,可能有非常大的潛力,要多給它們一些機會表現。至於這個演算法為什麼叫置信上限,算出來的分數其實就是一個置信區間(Confidence intervals)的上限。
同樣地三台老虎機不設定探索率改 UCB 策略: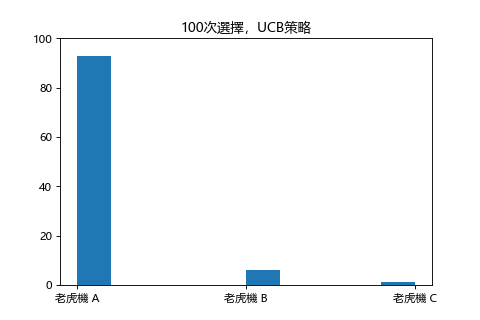
雖然有了策略,但要找出累積報酬最大的策略其實是很難的,所以加入了價值的概念,針對狀態給價值,選擇可以往高價值的狀態移動的行為。
一般說的價值函數指的是 Q 函數,Q 表示
狀態下
動作的品質(Quality)。
這邊用迷路問題舉例:
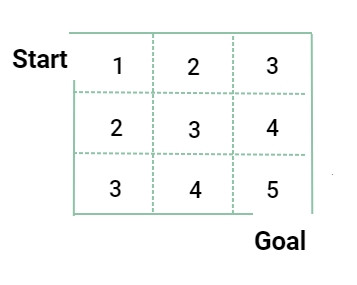
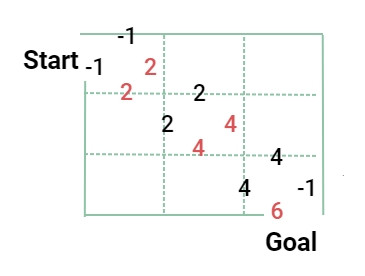
為了做出最好的決策,找到最大值的 Q 值,也就是最佳化 Q 函數的方法,叫做 Q 學習(Q-Learning)。
除了使用價值函數,也另外發展出用策略函數去求解最大累積報酬的方法。策略梯度就是用一個函數表示策略,然後透過梯度提升調整裏頭的參數(parameter)找到一個最佳的參數讓報酬最大化。
梯度提升是監督式學習的一種演算法,Day 8有介紹過,可以回顧加強印象。
常用的具體方法有:
REINFORCE 全名是 REward Increment = Non-negative Factor x Offset Reinforcement x Characteristic Eligibility
